El nuevo agente acelerador del crecimiento económico son las matemáticas: la ciencia más abstracta no solo ocupa el epicentro de la revolución digital, sino que es el poder invisible que aumenta la productividad en todos los sectores. El primer estudio que mide la “intensidad matemática” de la economía en España, realizado por Afi (Analistas Financieros Internacionales) por encargo de la Red Estratégica en Matemáticas (REM), concluye que las matemáticas son ya directamente responsables de “más de un millón de ocupados” el 6% del empleo total y de más del 10% del PIB”. Además, las profesiones intensivas en matemáticas son las que más crecerán en los próximos años. Pero el estudio también alerta de que el tejido empresarial español se nutre de menos matemáticas que el de los países del entorno, y que, si esto no cambia, la economía española perderá competitividad.
Las matemáticas son un bien “estratégico” que “acelera el crecimiento económico”, señala el nuevo informe, titulado Impacto socio-económico de la investigación matemática y de la tecnología matemática en España, que ha sido presentado esta mañana en Madrid, con la presencia de la ministra de Industria, Comercio y Turismo y una amplia representación de la empresa y de la comunidad de investigación matemática.
Nunca antes se ha cuantificado el peso de las matemáticas en la economía española, y de hecho no existe una metodología estándar para hacerlo. Pero los promotores del informe lo consideran indispensable, tanto para la industria como para los decisores públicos: “Las matemáticas se ven como algo en lo que investigamos unos cuantos académicos alejados de la realidad cotidiana, pero lo cierto es que son cada vez más un recurso nacional estratégico”, afirma Tomás Chacón, de la Universidad de Sevilla y coordinador de la REM, una red de conocimiento que integra a toda la comunidad matemática española y busca promover la transferencia de resultados matemáticos al tejido empresarial.
“Aplicar las matemáticas a todos los sectores económicos es lo que está dando ventaja a los países en los mercados, y ahora, por primera vez, tenemos los números que lo demuestran”, añade Chacón.
A la vista de las conclusiones del trabajo los propios matemáticos se declaran sorprendidos: “El impacto de las matemáticas en términos de valor económico y empleo alcanza valores sorprendentes”, escriben en el prefacio. Las matemáticas añaden valor “por supuesto en los modernos servicios digitales, comunicaciones e internet”, pero su uso se expande velozmente también “en sectores más convencionales”. Además, “las ramas económicas que más usan matemáticas son las más productivas y las de mayor perspectiva de crecimiento”.
Con este estudio los matemáticos españoles han querido aproximarse a ámbitos de los que han estado tradicionalmente alejados: la empresa y los jóvenes. “En países muy dinámicos económicamente hay mucha más transferencia de conocimiento matemático a la industria”, dice Guillermo Curbera, de la Universidad de Sevilla, responsable del estudio por parte de la REM. “A los chicos y chicas queremos decirles que si les gusta crear matemáticas ahora también pueden hacerlo resolviendo retos de la industria, aplicando su potencia intelectual y su creatividad al ámbito productivo, que es una de las fuentes más ricas de problemas”.
Medir un recurso invisible y sin dueño
Para llevar a cabo el estudio los expertos de Afi se inspiraron en los escasos precedentes conocidos de trabajos similares en otros países, en concreto los realizados por Deloitte en Reino Unido (2012) y Países Bajos (2014), y por la consultora CMI en Francia (2015). Emplear la misma metodología de estos estudios ha permitido comparar los resultados entre países. El estudio realizado por Afi ha completado dicha metodología con el enfoque que la Fundación Telefónica (2012) otorgaba a la estimación del valor económico del español, dada la similitud que hay entre ambas disciplinas.
La propia metodología, y adaptarla al caso español, ha sido un reto en sí mismo, por los peculiarísimos rasgos de las matemáticas entendidas como recurso. Las matemáticas, explica el estudio, son especiales sobre todo por tres razones: no son de nadie; cuantas más personas las usan más valor adquieren; y son casi siempre invisibles en el producto final, a pesar de que también son ubicuas están casi en todas partes.
Estas características generan “fallos de mercado”: “Al no ser un recurso apropiable no existe un valor de mercado. Los sistemas de contabilidad nacional solo miden bienes privados, es decir, aquellos que tienen asignado un precio de mercado. (...) Que la investigación y transferencia tecnológica matemática no tenga un valor de mercado dificulta la medición de su peso en la economía española”, indica el informe.
Pero difícil no significa imposible. La metodología aplicada por Afi sortea este obstáculo considerando no las matemáticas en sí, sino los beneficios para quienes poseen y aplican el conocimiento matemático en sus actividades. Así las matemáticas se entienden como un bien privado que sí es cuantificable con las métricas al uso, puesto que los “salarios y beneficios” atribuibles a la matemática figuran en la información estadística de las instituciones públicas.
Expresado en términos no técnicos, para determinar estos valores Afi logró medir cuántas matemáticas usan en su conjunto los trabajadores españoles, y combinó esos datos con cuántas matemáticas encierran determinados productos. Analizó para ello el mercado de trabajo español empleando los microdatos de la EPA (Encuesta de Población Activa) con el detalle de hasta 170 ocupaciones diferentes, y moduló los resultados con opiniones recabadas en entrevistas personales a una veintena de expertos en transferencia matemática, tanto en centros de investigación como en la empresa.
Un millón de empleos
Su análisis revela que el impacto directo en empleo alcanza el millón de ocupados, lo que representaría alrededor del 6% del empleo total de la economía española en 2016.
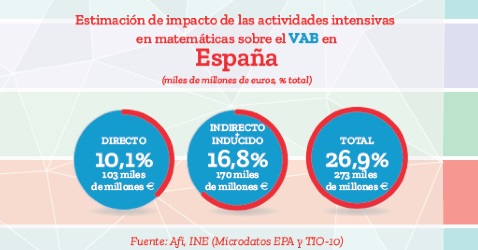
Esta cifra, y el conocimiento de la productividad por hora en cada uno de los 63 sectores Económicos contemplados en la EPA, permite conocer el PIB generado por las actividades con intensidad matemática: el 10,1% del PIB español total en 2016.
Pero las actividades intensivas en matemáticas ejercen además impactos indirectos, por ejemplo sobre la cadena de valor en su sector; e inducidos -el uso de las rentas derivadas de las actividades intensivas en matemáticas-. Si se contabilizan estos impactos, las matemáticas están detrás, en mayor o menor medida, del 19,4% del total de los ocupados en 2016, y generan el 26,9% del PIB total.
El informe muestra que las matemáticas afectan a todos los sectores, en las distintas fases del proceso productivo: desde el diseño, modelaje, simulación y prototipado de productos, a la optimización de procesos productivos y de organización y el análisis de datos. Por áreas, no obstante, las más intensivas en matemáticas son la informática, las actividades financieras, los servicios de telecomunicaciones y la rama de energía eléctrica y gas.
“Muy rezagada en profesiones de intensidad matemática”
Son datos que confirman la importancia económica de las matemáticas, pero que sitúan a España por detrás del Reino Unido, Francia y Holanda. Si en España las matemáticas son responsables directas del 6% del empleo total, en estos países la cifra oscila entre el 10% y el 11%. En cuanto al VAB, entre el 13% y el 16% del PIB total Reino Unido, Francia y Holanda es directamente atribuible a las matemáticas (10,1% en España).
Esta distancia “no sorprende en absoluto” a los autores del informe, que la atribuyen a “la diferente composición de la estructura productiva de la economía española” y a su “menor competitividad”, En concreto, “España destaca por estar muy rezagada en profesiones de intensidad matemática, como especialistas en bases de datos y redes informáticas, finanzas, profesionales de las tecnologías de la información o diseñadores de software y multimedia”.
Según Eurostat, en España alrededor del 30% de las ocupaciones son intensivas en matemáticas, mientras que la media de la Unión Europea-15 está en el 40%.
No son muy buenas noticias de cara al futuro, porque según la agencia de la Unión Europea Cedefop (Centro Europeo para el Desarrollo de la Formación Profesional), las previsiones de crecimiento de las ocupaciones intensivas en matemáticas para entre 2015 y 2025 son menores para España (0,47% anual) que para la Europa de los 15 (0,59% anual), “lo que ampliaría la diferencia actual”, señala el informe. “Eso a pesar de que las perspectivas de crecimiento del empleo para estas profesiones más que duplica las del resto de ocupaciones”.
Más formación matemática, más crecimiento
El estudio se completa con la mirada a otros indicadores también informativos de la relación entre matemáticas y economía, como el número de publicaciones científicas en el área de investigación matemática, o el de graduados en carreras de ciencia y tecnología (STEM, por sus siglas en inglés). Un análisis de 66 países halla “importantes efectos positivos de estos indicadores en la productividad de los trabajadores”, señala el informe.
En concreto, se estima que “si España incrementase la proporción de graduados STEM sobre el total de la población al mismo nivel que en Francia, la productividad del trabajo podría aumentar en un 2,2% sobre los valores actuales”.
El informe concluye con recomendaciones de política pública dirigidas al ámbito de la educación, a los propios matemáticos y a los gestores económicos y de I+D+i: más presencia de las matemáticas en los programas educativos; más comprensión por parte de los matemáticos de la aplicabilidad de sus conocimientos; aproximar los centros de investigación matemática al tejido empresarial; impulsar el gasto en I+D+i en las ciencias matemáticas; incrementar los incentivos a las matemáticas aplicadas; y visibilizar en el entorno empresarial las ventajas que reporta la incorporación de matemáticos.
Exactamente qué aportan las matemáticas
Las matemáticas participan de manera transversal en la actividad productiva, pues inciden sobre todos los sectores, en tres ámbitos clave:
1) Diseño, modelaje, simulación y prototipado de productos. Las matemáticas añaden mucha precisión a la fabricación de bienes y servicios. Un ejemplo es la automoción, donde las matemáticas han sido un instrumento fundamental para la mejora de los vehículos.
2) Optimización de procesos productivos y de organización. Las matemáticas reducen costes de transacción internos y externos, y mejoran la eficiencia (producir al menor coste posible). Aplicadas a la logística industrial, por ejemplo, optimizan la red de distribución (almacén, reparto, ruta, planificación de los horarios, desplazamientos, etc.).
3) Análisis de datos. Gracias a las matemáticas la información adquiere sentido económico y es aprovechable (por ejemplo, mediante técnicas de Big Data). Por ejemplo, en aeronáutica, el análisis de grandes volúmenes de datos permite mejorar la eficiencia de los vuelos (consumo de combustible, emisiones, tiempos de vuelo, retrasos, etc.).
Un bien público ‘de club’ más valioso cuanto más se invierte en educación (o cómo sale de rentable la educación matemática)
Los teoremas no son patentables, y sin embargo están en la base de la pirámide de ideas y conocimiento aplicado a las actividades productivas. Las matemáticas son desde ese punto de vista un bien “no rival”, porque la aplicación de un teorema no agota las posibilidades de uso por parte del resto de los ciudadanos. Además son un bien de club, dado que solo poseen el recurso quienes conocen el lenguaje matemático: al club de las matemáticas se accede con aprendizaje. Sin embargo, a diferencia de la mayoría de los bienes públicos de club, este no presenta economías de congestión, sino de adopción o red: cuantos más usuarios, más valor.
En otras palabras, cuanta mayor formación matemática tenga una población, más rico será su club matemático y más se beneficiará su tejido productivo. Este mensaje, relevante para los responsables de políticas públicas, se puede incluso expresar en cifras: “Se estima que la mejora de la educación matemática desde edades tempranas genera una rentabilidad en términos de mejores ocupaciones y mayores salarios en el futuro que oscila entre el 7% y el 10%”, afirman los expertos de Afi.
Como explica el informe, las matemáticas son “un activo que portan los individuos, que precisa de una inversión inicial en aprendizaje y que a lo largo de la vida del individuo le generan beneficios tangibles. (...) Así pues, cuanto mayor sea el apoyo público para disminuir los costes de aprendizaje, mayor será el incentivo a extender el stock de conocimiento matemático entre los individuos de una comunidad”.
‘Cómo se hizo’
La metodología combina dos enfoques, el de ocupaciones y el de producto. En las ocupaciones se identifican las ocupaciones con intensidad matemática a partir de las ocupaciones identificadas en otros estudios europeos; con los microdatos de la EPA (INE) -selección de disciplinas matemáticas e identificación de ocupados que han completado diferentes niveles educativos en dichas disciplinas-; y contrastando con expertos en transferencia matemática. También se ha analizado la distribución sectorial de las ocupaciones con intensidad matemática.
En el enfoque de productos se analiza la tabla de origen y destino de las TIO-2010 para identificar el valor económico de la producción de productos con intensidad matemática.
Para cuantificar el impacto directo en PIB -el informe lo hace en VAB, Valor Añadido Bruto, una magnitud equiparable al PIB ya que tan solo tendrían que añadirse los impuestos netos sobre los productos-, se identifica la productividad laboral de los sectores económicos en que trabajan los ocupados intensivos en matemáticas y se multiplica por el número de ocupados intensivos en matemáticas y el tiempo efectivo dedicado a dichas tareas.
La cuantificación del impacto indirecto e inducido en empleo y PIB (VAB) se realiza con las tablas Input – Output, ya que permiten calcular los multiplicadores de empleo y VAB de las actividades en las que trabajan los ocupados intensivos en matemáticas sobre otros sectores económicos.
Matemáticas y crecimiento acelerado
Las matemáticas son “una herramienta esencial para el impulso de la productividad del trabajo, que es el determinante fundamental del crecimiento económico en el largo plazo”, señala el informe. “Además, al ser un bien no rival, los beneficios económicos de su uso pueden ser proporcionales a la población, impulsando así procesos de crecimiento muy acelerado, como el que viene observándose en China en las últimas tres décadas”.
Además las matemáticas son indispensables para “la generación de ecosistemas empresariales, el fomento de la inversión y la competitividad y, sobre todo, el impulso de la innovación”, prosigue el informe.
El precio de los bienes de capital con aplicaciones matemáticas, sobre todo los relacionados con la información y la comunicación, se ha reducido mucho en los últimos años, lo que facilita su utilización masiva incluso por quienes no tienen conocimientos matemáticos avanzados. Esto “podría estar facilitando una difusión más rápida de la tecnología y, en definitiva, un crecimiento mayor en las economías en desarrollo”, apuntan los expertos, en referencia no solo al hardware -ordenadores, móviles- sino las aplicaciones informáticas o plataformas digitales, cuyo uso se extiende cada vez más -generando valor a la economía- y que basan su funcionamiento en algoritmos ocultos.
Casos de éxitos
SEAT optimiza la distribución de automóviles con matemáticas
Cada día, más de 2.000 coches nacen en la fábrica de SEAT en Martorell, y parten hacia destinos distribuidos en 75 países. Cada vehículo es único, con características escogidas de antemano por un dueño que ansía su llegada. Para SEAT, optimizar ese proceso de distribución supone no solo acortar tiempos de espera en los concesionarios, sino también aprovechar mejor el espacio que ocupan miles de coches aparcados. “Un coche ocupa entre 15 y 20 metros cuadrados, por lo que un solo día de stock son 40.000 m2”, dice Manuel Medina Burrull, responsable de Distribución en SEAT.
Medina Burrull decidió recurrir a las matemáticas para mejorar la predicción de cuándo estarían disponibles los coches. No era un reto sencillo, teniendo en cuenta que implica modelar un proceso de fabricación con miles de variables –desde la disponibilidad de cada pieza hasta el color del automóvil- y también que cada coche debe ser enviado a un destino específico, donde está su cliente -como dice Burull, “Un coche no es intercambiable con ningún otro”-. Pero el resultado ha valido la pena.
Después de varios meses de trabajo con la compañía Kernel Analytics SEAT está ya desarrollando un modelo matemático que en la fase de prueba de concepto anticipa en dos días la información sobre lotes de transporte. Su aplicación completa deberá acelerar al menos también en dos días la salida de los coches de la fábrica. El modelo estará integrado con una herramienta informática de comunicación con toda la cadena de distribución.
El próximo paso de Distribución de SEAT, en su acercamiento a las matemáticas, será un estudio sobre el impacto de los diferentes elementos de coste en la cadena de distribución. Distribución de SEAT ya ha iniciado contactos con el CRM (Centre de Recerca Matematica vinculado a la Universitat Autonoma de Barcelona) para este desarrollo.
GMV mejora la precisión del sistema Galileo
Galileo es el sistema global de navegación por satélite de la Unión Europea. Estará oficialmente completado en 2020, pero con 26 satélites en órbita proporciona ya información de posicionamiento combinable con la de los satélites estadounidenses GPS. La compañía española GMV ha desarrollado para Galileo un método de estimación de la posición y relojes de los satélites con una precisión muy superior a la de los otros sistemas de navegación.
En los sistemas de navegación global los satélites funcionan como relojes muy precisos, que transmiten “marcas de tiempo” a través de señales electromagnéticas mientras orbitan la Tierra. El receptor recibe los tiempos de los satélites y los compara con el suyo; sabiendo la posición de tres satélites y lo que tarda la señal en cubrir la distancia satélite-receptor, se calcula la posición de este último. En la práctica, sin embargo, alcanzar la máxima precisión no es sencillo, y es justo lo que ofrece Galileo: un servicio más preciso y garantizado, indispensable para aplicaciones como los vehículos sin conductor, por ejemplo. Para lograrlo es fundamental estimar de forma muy precisa la posición de los satélites y sus relojes. GMV, uno de los contratistas más importantes de Galileo, ha desarrollado un método que lo permite.
Para Esther Sardón, matemática responsable de la División de Sistema Operacional de Galileo de GMV, es un éxito basado en la capacidad de resolver problemas: “No se trata de aplicar aplicaciones que ya existen, aquí tenemos que dar un paso más allá, no está todo hecho”, afirma”.
El impacto de los sistemas de navegación por satélite en la economía global es importante. Hay un impacto directo, que se puede contabilizar con indicadores como la venta de receptores de navegación, y un impacto indirecto, considerando que los sistemas de navegación son un elemento esencial en muchos de los desarrollos tecnológicos actuales más innovadores, como son el internet de las cosas, el “big data”, la realidad aumentada, las ciudades inteligentes y la logística multi-modal.
Matemáticas para diseñar encajes
Hace más de tres décadas que la empresa CADT desarrolla y perfecciona programas para la industria textil. Su software de diseño fue creado para la industria del encaje, cortinas, puntas, “en general el género de punto que tenía una industria muy potente en Cataluña en los años 70-80”, explica Pascual Castellón, de CADT.
El programa ayuda en la puesta en carta, es decir, la transformación digital de un dibujo artístico para que sea aceptado por la máquina textil. Es un trabajo muy técnico y especializado debido a la metodología del género de punto, y tiene aplicaciones en lencería, vestidos de novia, cortina, puntillas…”. En CADT los diseñadores transmiten a los programadores sus necesidades, y los programadores piden a los diseñadores que prueben los nuevos programas y les informen de los problemas antes de lanzar el producto al mercado.
“En un programa de diseño las matemáticas aparecen continuamente, y en especial la geometría”, señala Castellón. “En un momento determinado desarrollamos una librería gráfica específica para el programa usando primitivas para dibujar figuras geométricas, interpolación de líneas, trazo de arcos, manipulación de matrices para realizar cambios de coordenadas, e implementamos algoritmos de tratamiento de imágenes. En el futuro, con la introducción de nuevas tecnologías que nos gustaría incorporar al programa como la Inteligencia Artificial y/o Machine Learning, esperamos que las matemáticas tengan una presencia aún más importante”.
Medir fácilmente la densidad de la sangre para detectar enfermedades
RheoDx desarrolla un dispositivo diagnóstico portátil capaz de detectar de forma inmediata y económica las anomalías de las células sanguíneas mediante una sola gota de sangre. Dirigido a un mercado de 80 millones de personas en Europa, mejora la eficiencia en el seguimiento de pacientes con enfermedades hematológicas incluyendo anemias, cánceres líquidos, trastornos de coagulación e infecciones como la malaria. En concreto, el aparato es un reómetro que mide la viscosidad de los fluidos en movimiento, en este caso la sangre, y convierte estos valores en una función. Cada función se corresponde con una patología, y así se realiza el diagnóstico. El proyecto nació en el Centre de Recerca Matemática (CRM) de la Universitat de Barcelona.
Pero RheoDx desarrolla un microreómetro, que determina viscosidad a partir de muestras muy pequeñas gracias a las matemáticas. Los modelos matemáticos que describen la viscosidad son funciones que relacionan presión y velocidad. El reómetro aplica una serie de presiones sobre el fluido, y anota las velocidades asignadas a cada una de ellas; así traza la función viscosidad. Dado el reducido volumen de muestra, se necesita muy alta precisión para trazar la función. Para ello, la herramienta matemática cruza grandes familias de funciones similares que se optimizan simultáneamente en función de las lecturas experimentales del reómetro, hasta encontrar los parámetros más exactos que satisfacen a todas ellas y que darán por resultado la expresión final del modelo de viscosidad de la muestra.
El microreómetro aspira a ser similar al termómetro, pero para la viscosidad de la sangre: igual que a la temperatura corporal informa acerca de diversas patologías, un sistema pequeño y barato para medir la viscosidad de la sangre puede convertirse en un práctico instrumento médico.
Ghenova: un trazador de rutas para tuberías y canalizaciones en barcos
Trazar el recorrido óptimo de tuberías de drenaje o canaletas eléctricas puede ser el mismo problema que trazar la mejor ruta en un crucero. Hay puntos de paso obligado -enchufes o grifos… o puertos turísticos- y otros a evitar, y a la vez se intenta recorrer la menor distancia posible. El problema es todo menos sencillo. La compañía Ghenova se propuso como proyecto de I+D conseguir un algoritmo trazador de rutas.
Tras varios años de trabajo en colaboración con matemáticos del Instituto de Matemáticas de la Universidad de Sevilla (IMUS), los resultados se presentaron en un congreso de ingeniería naval en 2017. Se interesó por el proyecto SENER, autor del programa de diseño naval FORAN -una herramienta comercial de software naval empleada en el mundo entero-. Con el apoyo de varias instituciones públicas se dispone ya de una herramiento de uso interno, próximo a convertirse en producto comercial. Hasta ahora el trazado de las rutas lo hacen personas (con ayuda de asistentes 3D) con una enorme carga de trabajo y tiempo. El nuevo programa resuelve el problema en menos tiempo, y redefine el proceso de trabajo al completo.
Grupo Ferroglobe: Estrategia de Producción Eficiente de Silicio
El Grupo Ferroglobe, en colaboración con el Instituto Tecnológico de Matemática Industrial (ITMATI), ha estudiado un horno industrial destinado a la purificación de silicio solar para mejorar su eficiencia y productividad mediante la simulación numérica de los procesos que tienen lugar en su interior, mediante la simulación numérica integral del conjunto de procesos físicos acoplados (electromagnéticos, térmicos, hidrodinámicos, termodinámicos y estructurales.
Se ha logrado una herramienta que le permite optimizar el proceso evitando las pruebas ensayo-error en planta, que son técnica y económicamente muy costosas.
Además, se ha incorporado a la herramienta de simulación el modelo estructural que permite estudiar con detalle las partes de la máquina sometidas a mayor estrés térmico y mecánico, entender el origen de deformaciones y daños en el material y diseñar alternativas sin comprometer el rendimiento del proceso.
Un enjambre anti-incendios de medios aéreos tripulados y no tripulados
El proyecto ENJAMBRE, en el que el ITMATI colabora con la empresa Coremain, desarrolla tecnologías para optimizar la extinción de incendios, de forma que se reduzca la superficie afectada y aumente la seguridad de las brigadas anti-incendios. El objetivo principal es el desarrollo de sistemas inteligentes para el control avanzado de trayectorias, que permita la operación cooperativa entre aeronaves tripuladas y de observación. El grupo de ITMATI ha generado además bases de datos con información relevante -sobre el territorio, el tipo de combustible en el momento de un incendio, las aeronaves implicadas en tareas de extinción-, y ha desarrollado algoritmos para estimar parámetros clave, como el perímetro del incendio; los frentes de llama; y los focos.
También se ha logrado es estimar el flujo de calor por radiación que emite el frente de llama, incidiendo sobre un receptor para evitar quemaduras y dolor al ser humano: se representa en un mapa el flujo de calor desde el frente de llama a distintas distancias y en todas las direcciones, y así el brigadista sabe a qué distancia máxima puede aproximarse. Se ha desarrollado además un algoritmo para el cálculo de rutas de escape para las brigadas. El objetivo es calcular una ruta de escape para la evacuación de los medios de extinción terrestres, de forma que se le proporcione al director de extinción una ruta de escape segura para retirarse desde el incendio hasta el destino seleccionado.





 Si (
Si ( No(
No(





















